Učinkovitost vlakana u mikroarmiranim betonima – čvrstoća prijemčivosti i izvučna sila vlaka
Ocjena učinkovitosti vlakana koja se koriste u mikroarmiranim betonima iznimno je važna pri izvedbi običnog industrijskog poda pa ćemo zato ovo poglavlje obraditi opširnije, a sama će se tema nastaviti i u sljedećem broju časopisa.
Uporabom X – zraka otkriveno je da se raspukline na dodirnoj površini: cementna pasta – zrno agregata, pojavljuju pri postizanju 30% napetosti od čvrstoće na tlak kod betona. Raspukline u matrici pojavljuju se kod nešto više napetosti.
Udruživanjem tih pukotina nastaje glavna raspuklina, koja ima vijugast oblik, jer se pukotine često ugibaju zrnima agregata. Uporabom elektronskog mikroskopa kod pomno nadziranih pokusa sa silom na vlak bilo je otkriveno, da »kraj« raspukline teži razvijanju te da započinje u cementnom kamenu kod zrnaca pijeska, a i to da su raspukline često diskontinuirane. Krivudanje raspuklina na mikroskopskom nivou razlaže se sa takvim učinkom, da se tijekom procesa lomljenja betona zrna agregata ‘ispušuju’ iz cementne matrice, jer ona najčešće imaju veću tvrdoću od cementnog kamena te od veze između cementnog kamena i zrna. Povećanje žilavosti betona na slamanje putem cementne paste vjerojatno proizlazi iz ispušenja agregatnih zrna ili učinka premoštenja. U mikroarmiranom betonu prevladava učinak premoštenja zahvaljujući vlaknima. To je rezultat ispušenja ili trganja vlakana i na taj se način uvećava duktilnost mikroarmiranog betona.
ČVRSTOĆA PRIJEMČIVOSTI (PRIHVATA) I IZVUČNA SILA VLAKA
Uzajamno djelovanje vlakana i matrice je osnovna osobina koja utječe na ponašanje mikroarmiranog kompozitnog materijala. Razumijevanje tog uzajamnog djelovanja je potrebno za ocjenu doprinosa vlakana i predviđanja vezana uz ponašanje kompozita. Uzajamno djelovanje vlakana i neraspucale matrice ima u aplikaciji ograničeno značenje, jer će u najvećem broju slučajeva matrica od uporabe puknuti. Studija ovih međusobnih djelovanja daje korisne informacije za razumijevanje cjelovitog ponašanja kompozita. Osim toga, neraspucali dijelovi konstrukcije utječu na cjelovito ponašanje konstrukcijskog sustava, posebno kada se u kompozitu već razviju pukotine.
Na slici 1 je prikazan jednostavan sastav vlakno – matrica, koji sadrži pojedinačno vlakno. U slučaju kad ne djeluje opterećenje, pretpostavlja se da je napetost u matrici i vlaknu jednaka nuli (slika 1a). Kad na kompozit djeluje opterećenje na vlak ili tlak, ili kad na njega djeluje promjena u temperaturi, pojavljuju se napetosti i deformacije koje moraju ostati kompatibilne. Već i sama hidratacija cementa može uvesti napetosti kako u matricu, tako i u vlakna. Kad opterećenje djeluje na matricu, dio tog opterećenja se prenosi na vlakno duž njegove površine. Zbog razlike u ukrućenosti, između vlakana i matrice stvara se napetost na posmik duž površine vlakna. Ova napetost na posmik djeluje tako, da se dio opterećenja prenosi na vlakno. Ako je vlakno ukrućenije od matrice, deformacija na i u okolini vlakna će biti manja, kao što je prikazano na slikama 1b i 1c. Takav je slučaj kod čeličnih i mineralnih vlakana. Ako je modul elastičnosti vlakna manji od modula elastičnosti matrice, deformacija u okolini vlakna bit će veća. To možemo vidjeti u slučaju kompozita sa polimernim i nekim prirodnim vlaknima.
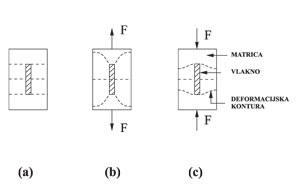Slika 1: Uzajamno djelovanje vlakno – matrica (neraspucala matrica): (a) bez opterećenja, (b) vlak, (c) tlak.
Prijenos napetosti je elastičan u neraspucalom kompozitu onoliko vremena dok se matrica i vlakno nalaze unutar elastičnog područja napetosti. Dijagram matrice s – e može iskazati nelinearnost i neelastično ponašanje kod loma. Razvijene su i matematičke jednadžbe za napetost na posmik na dodirnoj površini t te napetost uzduž vlakna. Ovi se modeli obično nazivaju modelima preostalog posmika. Zasnovani su na brojnim pojednostavljenim pretpostavkama. Te pretpostavke uključuju:
- linearno elastično ponašanje vlakna i matrice,
- potpunu vezu između vlakna i matrice,
- dodirna površina je ekstremno tanka i njeno je svojstvo jednako svojstvu matrice na drugome mjestu, i
- vlakna imaju glatke i pravilne poprečne presjeke.
Raspodjela napetosti na posmik t(x) u razmaku x od kraja vlakna izražava se kao:
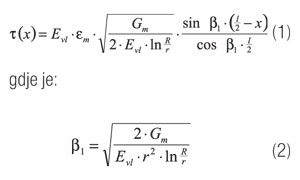
Odnos je funkcija prostornog udjela vlakana i rasporeda vlakana. Razvijeni su izrazi za kvadratne i heksagonalne rasporede vlakana. Napetost u osi vlakna svl(x) može se izračunati iz sljedeće jednadžbe:
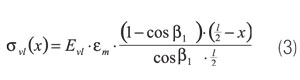
Raspoređivanje napetosti na posmik t(x) i normalne napetosti svl(x) vrši se nelinearno duž vlakna. Potrebno je naglasiti da u ovim jednadžbama nisu bili uključeni Poissonovi efekti. Unatoč tome, jednadžbe (1) do (3) na temelju postavljenih, vrlo ograničenih pretpostavki pružaju mogućnost izračuna napetosti u vlaknima i njihov utjecaj na kompozit.
U praktičnim slučajevima vlakna su proizvoljno raspoređena u najmanje dvije dimenzije. U mikroarmiranim betonima su vlakna proizvoljno raspoređena u sva tri (međusobno pravokutna) smjera. Pored toga, većina čeličnih vlakana i neka polimerna vlakna imaju i namjerno deformirane površine ili krajeve. U gotovo svim slučajevima postoji međusobno djelovanje vlakana, što dodatno povećava složenost problema. Radi toga su matematički modeli za praktičnu primjenu još uvijek u – početnom stanju razvitka.
Prema ponašanju kompozita kod različitih stanja opterećenja može se utvrditi da li vlakna doprinose čvrstoći i ukrućenosti kompozita. Sa kakvim osobinama i koliki će biti njihov doprinos – ovisit će o vrsti i prostornom udjelu vlakana te o osobinama matrice. Na primjer, kompozit koji sadrži 10 vol. % čeličnih vlakana ima peterostruko povećanje čvrstoće na vlak, ali je to povećanje minimalno kod prostornog udjela manjeg od 2 vol.%.
Ako je mikroarmirani kompozit opterećen na vlak (slika 1b), matrica će na određenom stupnju opterećenja – puknuti. (Slika 2).
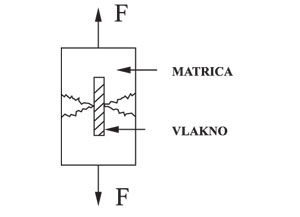Slika 2: Uzajamno djelovanje vlakno – matrica (raspucala matrica).
Kad matrica pukne, vlakno preuzima opterećenje prenoseći ga kroz raspuklinu s jedne strane matrice na drugu stranu. U praktičnom slučaju će više vlakana premostiti raspuklinu prenošenjem opterećenja. Ako vlakna u cijelosti prenose opterećenje kroz prvu pukotinu, duž nje će se oblikovati još više raspuklina. To stanje opterećenosti naziva se stanjem višekratne raspucalosti. U mnogim primjenama se ovo stanje višekratne raspucalosti događa u uvjetima stalne opterećenosti. Graničnu nosivost i ponašanje kompozita kod maksimuma isto tako određuju karakteristike djelovanja vlakana.
Najvažnija pitanja u vezi sa djelovanjem vlakana su:
- varijacije opterećenja – klizanje
- utjecaj geometrije i orijentacije,
- kako ocijeniti otpor na vlak za pojedinačno vlakno,
- uzajamno djelovanje proizvoljno raspoređenih vlakana, sa svrhom ocjene višekratnog izvlačenja vlakana.
Veza između vlakna i matrice može se proučavati na temelju podataka dobivenih izravnim i neizravnim pokusima. Neizravnim pokusima kompozit se iskušava na vlak ili savijanje te se ocjenjuje doprinos vlakana. Potom se vrši opširna matematička analiza da bi se utjecaj vlakana razlučio od utjecaja matrice. Rezultati dobiveni ovim postupcima vrlo su ovisni o matematičkom modelu koji se koristi kod analiziranja.
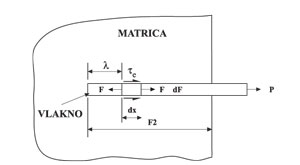
Mehanizam gubitka prijemčivosti na spoju vlakno – matrica je važan parametar za razumijevanje veze opterećenje – klizanje. Vrlo značajnu ulogu ima spoj vlakno – matrica nakon raspucavanja matrice. Shematski prikaz ocjene izvlačenja pojedinog vlakna prikazan je na slici 3.
Slika 3: Shema rješenja izvlačenja vlakna, koja prikazuje definicije parametara modela.
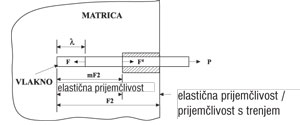
Kako je opterećenje malo, prihvat ili prijemčivost može se iskazati kao pojava elastičnosti. Napetost na posmik može se izračunati po teoriji elastičnosti, odnosno rješavanjem jednadžbi ravnoteže, kompatibilnosti i graničnih uvjeta. Uz pretpostavku da se utjecaj vlakna širi do radijusa veličine uzajamne udaljenosti vlakana, može se napisati jednadžba za elastičnu napetost prihvata te, kako slijedi:
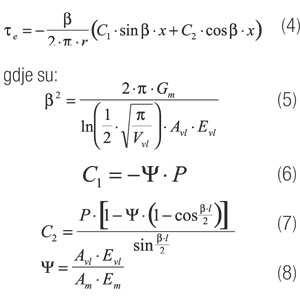
x – dužina, mjerena od kraja ugrađenog vlakna (slika 3).
Raspoređivanje napetosti na posmik, koja je izražena jednadžbom (4) rezultira u najvećoj napetosti na posmik na raspucaloj površini matrice. Kad ta napetost na posmik premaši čvrstoću posmika u vezi vlakno – matrica ts, dolazi do otvaranja raspukline. Pukotina napreduje uzduž vlakna (slika 3b). U zoni pukotine otpor trenja ti nudi i određeni otpor na vlak. Taj otpor trenja je manji od čvrstoće prijemčivosti matrice, a često se pretpostavlja da je konstantan (slika 4).
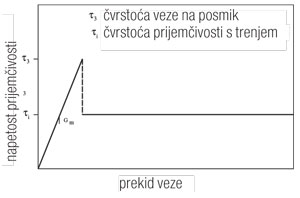Slika 4: Idealizirani dijagram osobina veze. Očevidno je potpuno elastično ponašanje, sve dok se ne dosegne čvrstoća veze na posmik ts, koja se nastavlja sa konstantnom prijemčivošću s trenjem ti .
U slučaju djelomičnog otvaranja raspukline, sila izvlačenja se može izraziti kao:
Na području od 0 do veza je elastična, no u području od do otpor predstavlja čisto trenje. Jednadžba (9) važi samo za čelična vlakna.
Ako je čvrstoća trenja ti manja od čvrstoće prijemčivosti ts, sila vlaka doseže maksimum već nakon stabilnog procesa otvaranje raspukline, kao što je prikazano na slici 5.
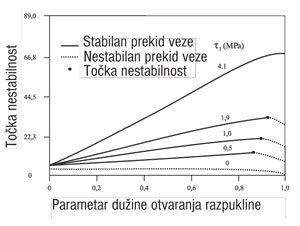Slika 5: Model sile vlaka u ovisnosti o parametru dužine otvaranja raspukline (1 – m), koji prikazuje stabilne i nestabilne režime otvaranja raspukline ovisno o odnosu (promjer vlakna = 0.4 mm, ugrađena dužina l/2 = 13 mm, ts = 4.1 MPa) .
To dokazuje da pokus sa silom vlaka pokazuje područje stabilnog otvaranja raspukline prije točke na kojoj se doseže granična čvrstoća. Poprečna krivulja s – e kompozita postaje nelinearna prvenstveno radi toga, jer se pokreće stabilan proces otvaranja raspukline prije izvlačenja vlakna.
Čvrstoća prijemčivosti ili prihvata općenito se izračunava uz pretpostavku ravnomjerne podjele napetosti na vezi . Najveća sila izvlačenja dijeli se sa dodirnom površinom vlakna i dobiva se čvrstoća prijemčivosti veze. Taj pristup se koristi za karakterizaciju čvrstoće prihvata u ovisnosti o dužini i promjeru vlakna. Alternativni pristup je uporaba dvo-parametarskog modela, uz uporabu ts i ti kao osobina materijala. Ta dva parametra bi se mogla nazvati i osnovnim osobinama materijala. Sila vlaka, koja se izračunava uz uporabu gore opisanog ponašanja, može se koristiti za predviđanje ponašanja mikroarmiranog kompozita kod opterećenja na vlak.
Istražuju se modeli na osnovi mehanike loma, kod kojih je proces popuštanja i izvlačenja modeliran kao razvitak raspukline neke veze. Koristi se energetski kriterij širenja raspukline. Energetski pristup je geometrijski neovisniji od pristupa preko stanja napetosti.
Jakob Šušteršič
